Rubber Sheet Geometry Definition

Topology branch of mathematics sometimes referred to as rubber sheet geometry in which two objects are considered equivalent if they can be continuously deformed into one another through such motions in space as bending twisting stretching and shrinking while disallowing tearing apart or gluing together parts.

Rubber sheet geometry definition.

The definition of a rubber is someone who massages something or slang for a condom. The calendar provides the dimensionality to the rubber compound by controlling the thickness gauge and width. A circle made out of a rubber band can be stretched into a square. An example of a rubber is a trojan brand condom.

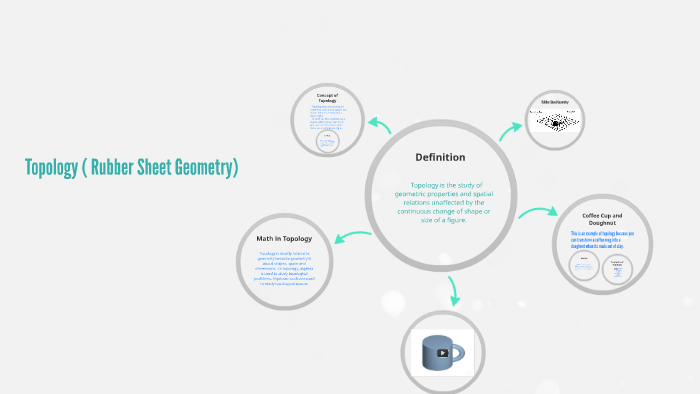
Topology rubber sheet geometry topology is the study of geometric properties and spatial relations unaffected by the continuous change of shape or size of a figure. During the rubbersheet adjustment junctions will move and drag any connected lines with them. Such shapes are an object of study in topology. Definition of a topological space a topological space x τ is a set x with a collection of subsets of x.

In a topology of two dimensions there is no difference between a circle and a square. To preserve the shape of linear features during the adjustment you should open the editing options dialog box click the general tab and turn on the option to stretch geometry proportionately when moving a vertex. An entry level primer on rubber sheet geometry. For example a square can be deformed into a circle without breaking it but a figure 8 cannot.

A möbius strip a surface with only one side and one edge. Noun an example of a rubber is a massuese. Topology has been called rubber sheet geometry. X and the.

Topology studies properties of spaces that are invariant under any continuous deformation.